10. エネルギーの大きいベータ粒子
図13.エネルギーの大きいベータ粒子
上のベータ粒子の飛跡の写真を見てください。今度は、前回と反対にCsのベータ線としては発生頻度が低い高エネルギーの場合です。矢印で示した長 く、ゆるやかにカーブする飛跡からベータ粒子のエネルギーを求め、この粒子がわれわれの体の中を運動していくときどのような物理的影響を及ぼすか、考えて みたいと思います。
図13の写真の中央の細く長いベータ粒子のエネルギーは、磁界の強さB=0.080Tのところで飛跡の回転半径R=5.0cmと測定できました。
図13では、ベータ線のスピードが大きくなっているので飛跡の曲率半径が大きくなっています。また、ベータ線の飛跡の濃さが高速になると飛跡が低速のときよりより相当うすくなっていることもわかると思います。
ベータ粒子の運動エネルギーと速度の計算の仕方は前回と同じなので、そのプロセスは省略し、以下にその結果のみ示します。
①ニュートン力学による計算
ベータ線の運動エネルギー:K=1.40MeV、
ベータ線の速度:u= 2.27×108 m/s
②相対性理論による計算
ベータ線の運動エネルギー:K=0.79 MeV
ベータ線の速度:u=2.3×108 m/s
①と②の計算結果を比較すると、今度は明らかな違いが出てきました。だんだんニュートン力学ではエネルギーの大きさの誤差が大きくなり始めました。 このあたりになると、計算は相対性理論で行かざるをえなくなりました。以下では、相対論の②の計算値で話を進めます。0.79MeVはセシウ ムからのベータ粒子のエネルギーとしてはかなり大きい値で、発生頻度はかなり小さいものです。
11.エネルギーの大きいベータ粒子の影響
ベータ線の飛程は写真では7㎝ほどしか見えていませんが、0.79MeVのエネルギーなので、もっと空気中を進んでいるはずです。調べてみると、空気中では2.5m 、体内(体内を水中で近似)では約3mm くらい進むことがわかりました。
(a) 外部被ばくの影響
このエネルギーの大きいベータ粒子は水中を3mm進むので、外部被曝では人間の皮膚に3mmくらい侵入します。0.79MeVのエネルギーをeVに直すと0.79×106eVとなり、このエネルギーでの細胞での化学結合の切断数Nは、1ヶにつき5eV消費するとするとN=0.79×106 / 5 =1.6×105ヶ=16万個 にもなります。
(b) 内部被ばくの影響
Csを体内に取り込んでしまい、線源が体内から、高エネルギーのベータ粒子を発射する内部被ばくした場合を考えてみます。
体内を水中とおいて0.79 MeVのベータ線の全飛程は、先ほどと同じ3mmです。化学結合の切断数も16万個と同じです。もし10ミクロンのサイズの細胞を0.79 MeVのベータ粒子が1ヶ通過するとすれば、細胞1ヶあたり500ヶの化学結合を切断していき、そのペースで300ヶの細胞にわたって繰り返し切断するエネルギーを持っています。
内部被曝の場合は、Cs原子が体内のどこかに一定の時間一定の場所に滞留しているので、半径3mmの球体の中心から繰り返しベータ線が放射されるこ とが起きます。そのため、外部被ばくと異なり内部被曝ではその球体内部に含まれる同一の細胞の化学結合の切断が繰り返される可能性があります。染色体が修 復に成功しても再び切断されたり、修復に失敗しながら生き延びた異常染色体が再び切断されていくことが起きる可能性が高くなります。こうした異常染色体は、がん細胞を解剖してみると、多数発見されることが報告されています。
(c) 高エネルギーと低エネルギーベータ粒子の比較
次に高エネルギーのベータ粒子と低エネルギーのベータ粒子のデータを使ってリスクを比較して見ます。さきに計算で得られた数値を利用して、エネルギーが小さいベータ粒子による被ばくの場合(0.028MeV)とエネルギーが大きい場合(0.79MeV)とで「細胞1ヶが受ける化学結合の切断数」がどう異なるか比較してみます。こでも具体例として中くらいのサイズの10μmの細胞で考えてみます。
・「低エネルギーのベータ粒子(0.028MeV)」が10μm細胞を横切るとき、2000ヶ切断する。
・「高エネルギーのベータ粒子(0.79MeV)」が10μmの細胞を横切るとき、530ヶ切断する。
- 図15 エネルギーが大きい場合((再掲) 図14 エネルギーが小さい場合(再掲)
細胞が受ける切断数の比を計算してみるとなんと4倍近くも低エネルギーの方の切断数が多いことが分かります。こうしたことから直感的に低いエネルギーのベータ線は高いエネルギーのベータ線より安全と考えがちですが内部被ばくにおいては逆であることがわかります。
12.霧箱で体内被ばくをイメージ化
(a) 霧箱でわかる化学結合の切断頻度
こうした内部被曝の様子や考え方を煩雑な測定や計算をすることなく、もっと簡単に分かる方法についてこれまでのまとめもかねて説明してみたいと思います。
ベータ粒子やアルファ粒子が霧箱の中(空気中)を通過すると、たくさん電離したり少量しか電離しなかったりさまざまですが、その電離の分量に応じ て飛跡が濃くなったり薄くなったりします。今度は、同じアルファ線やベータ線が生体内部を通過するときに、霧箱のときと同じようにたくさん電離したり少量の電離 したりしますが、今度はその分量に応じて、飛跡は形成されずに化学結合の切断がおきます。
霧箱内部では、放射線によって電離されたイオンを核にした巨大な凝結粒子とエアロゾルとよばれる無数の小さな凝結粒子とが混在しています。放射線の飛跡を構成する液滴はイオンを核とした巨大粒子が微少なエアロゾルを吸収合併して成長したものです。こうしたことから電離の分量と飛跡の濃さは、比例しているとみなせます。
他方、生命体の内部では、電離にほぼ比例して化学結合の切断量は増加します。(厳密に言うと、電離が起こらなくて励起だけでも切断が起こりますので、電離の分量以上に化学結合の切断は起きています。)こうしたことから放射線が霧箱の中に作る飛跡の濃淡を体内被曝での化学結合の切断の多少に置き換えることができます。もうすこし踏み込んだ言い方をすれば、飛跡が濃い場合ほど体内被曝において生体 に対するリスクが大きくなるケースに置きかえてもよいのです。
(b) 霧箱で体内被ばくをイメージ化
霧箱の飛跡の濃さは、放射線のエネルギーを消費し、その空間で電離している分量の大小を示しています。内部被ばくの場合には、飛跡はできませんがその空間で放射線のエネルギーを消費し電離していることは同じです。ただし、体内は霧箱の内部より物質の密度が約1000倍大きいので、エネルギーを失うまで放射線が進む距離が1000分の1も短くなるということは違います。
すでに説明したことですが、再度確認すると、霧箱の内部で50mm進んだアルファ線は、体内では50μmしか進みません。さらに体内では、電離によって発生した正イオンや負イオンで飛跡は形成せず、化学結合の切断がおきていきます。
こうしたことを考慮して、霧箱の内部で繰り広げられている現象を内部被ばくと置き換えて眺めてみてはどうでしょうか。飛跡の濃さは化学結合の切断量を示す分布図と解釈します。濃い飛跡では化学結合が(単長さあたり)多量に切断され、薄い飛跡では(単位長さあたり)少量になります。霧箱の5 cm の飛跡は50 μm が1000倍で拡大された映像と見なせます。
ビデオ映像や写真の中にうつしこんだ一辺が 1 cmの指標は10 μm の細胞の大きさと見なします。すると、飛程5 cm のアルファ粒子の飛跡は細胞 5 ヶ分(指標 5 ヶ分)をを横切って化学結合を切断していく様子を一望に見ていることになります。
数量的視点をいれたければ、アルファ粒子のエネルギーは核種によって多少の差がありますがせいぜい5~7MeVですので、1ヶあたりの化学結合の切断量は、すでにのべたとおりを5eVとして120万個~140万個と考えます。アルファ粒子が細胞5ヶ分を縦断していくとした場合、細胞1ヶあたり20~30万ヶの化学結合を切断していく、ということになります。
霧箱は起きている現象を平面で切り取ってみています。2次元の平面で起きている被ばくは、実際には3次元の立体で起きています。円形に広がっているベータ粒子は、実際には球面上に広がっていっています。
球の中心からランダムに発射する飛跡にそって化学結合の切断が起こります。外部被ばくと比べて狭い範囲で定点からの発射なので重複切断が発生する確率は飛躍的に高くなります。
[補足]:計算過程について
どういう風に計算をたどっていったのか、関心がある方のためにその概要を以下に述べます。
(a) 低エネルギーのベータ線の古典論でのエネルギーの計算
写真のベータ線の飛跡は、測定した曲率半径で円運動するとみなして電子の運動方程式をたてます。
m・(u2/R)=euB ―――――①
①式を変形してベータ線の速度uを使わないで運動エネルギーKをあらわす式に変形します。
運動エネルギーK= (1/2m) P2=(e2/2m)(RB)2 ―――――②
②式に数値を代入し計算をします。また、単位をJからKeVに換算するとK=29 KeV となります。
ここでベータ線の速度uを①式を使って計算してみます。
u=ReB/m=0.75×10-2×1.60×10-19×76×10-3 /9.1×10-31 =1.0×108 m/s
(b) 低エネルギーベータ線を相対性理論での計算
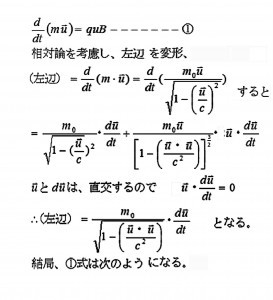
相対性理論からベータ粒子である電子についての運動方程式をたててみます。
d(mu )/dt=euB ――――――③
③式を変形していくと結局、運動量:P=ReBとなり、ニュートン力学と同じ式になります。
その証明の詳細は末尾に示しました。
運動エネルギーKの単位をMeVの単位にする都合から運動量の単位をMeV/cにすると④式になります。
P=ReB/(0.534×10-2) MeV/c=RB×3.00×102 MeV/c―――④
という簡潔な式が得られます。
④式にR,Bの値を代入しPを求めます。求めるKとPの関係式は以下の式⑤で表されます。
(0.511+K) 2=0.5112+(pc)2――――⑤
Pの値を⑤式に代入し、Kを求めます。するとベータ線の運動エネルギーは
K=0.02778 MeV =27.8KeV
となり低エネルギーの場合はニュートン力学で計算した値K=29KeVとほとんど差がないことがわかります。誤差は、4.3%です。